Minimax 博弈算法设计井字棋 AI(Golang)

Posted on | In

原文地址 zhuanlan.zhihu.com

Minimax 算法即极小极大值算法，是一种回溯算法，用于决策制定和博弈论。尤其是在双人之间的零和博弈中，假定两人都是绝对理性的情况下找出最佳决策方式。他广泛应用于两人回合制游戏，例如井字棋，国际象棋等。

在 Minimax 中，两人被称为最大化者和最小化者。最大化者试图获得尽可能高的分数，而最小化者试图做相反的事情并获得尽可能低的分数。

每个棋盘状态都有一个与之关联的值。在给定的状态下，如果最大化者占上风，那么棋盘的得分将趋向于某个正值。如果最小化者在该棋盘状态下占上风，那么它往往是一些负值。棋盘的价值是通过一些启发式计算的，这些启发式对于每种类型的游戏都是独一无二的。

评价函数

1
2
3
4
5
func evaluate(board [][]byte) int {
    var score int
    // 计算得失
    return score
}

对于双人零和博弈游戏来说，我必须首先制定一套根据实际状态计算双方得失的函数，我们称其为评价函数。 拿棋类游戏来举例的话，就是根据当前的棋盘状态 board 制定一套计算双方得失的规则，然后计算分数 score 返回。

minimax 函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func minimax(board [][]byte,depth int,isMax bool) int {
    /*
    board是当前棋盘状态
    depth当前递归深度
    isMax是回合布尔值
    */
    // 边界条件
    if /*终端状态*/ {
        return /*当前状态下的评价分数值*/
    }
    
    // 决策树的遍历
    if isMax {
        // 最大化者的最大化评价分数的选择
        score := -INFINITY
        for /*当前回合的所有状态*/ {
            // 状态假定选择
            // 选择撤销
        }
        return score
    } else {
        // 最小化者的最小化评价分数的选择
        score := +INFINITY
        for /*当前回合的所有状态*/ {
            // 状态假定选择
            // 选择撤销
        }
        return score
    }
}

max 最大化者代表我方，min 最小化者代表对手。我方要尽可能令评价分数最大化，对方要尽可能令评价分数最小化。

这个函数实质上就是对决策树进行遍历，返回对我方最有利，即评价分数最高的值。

最佳走法函数

1
2
3
4
5
6
7
8
9
10
11
// 决策（棋法）结构体
type Move struct {
    Position int
    ...
}
​
func findBestMove(board [][]byte) Move {
    var bestMove Move
    // 遍历当前回合的所有决策，寻找最大值
    return bestMove
}

利用 minima 函数返回最佳决策（走法）。

数学原理

$$
v_i = \mathop{max}\limits_{a_i} \ \mathop{min}\limits_{a_{-i}} \ v_i(a_i,a_{-i})
$$

$i$ 是当前玩家索引
$-i$ 是对手玩家索引
$a_i$ 代表当前玩家采取的行动
$a_{-i}$ 代表对手玩家采取的行动
$v_i$ 是当前局势状态的评估价值

$v_i$ 越是大的正数代表当前局势对于玩家 $i$ 更有利，$v_i$ 越是小的的负数代表当前局势对于玩家 $-i$ 更有利

minimax 算法伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
function  minimax(node, depth, maximizingPlayer) is
    if depth = 0 or node is a terminal node then
        return the heuristic value of node
    if maximizingPlayer then
        value := −∞
        for each child of node do
            value := max(value, minimax(child, depth − 1, FALSE))
        return value
    else (* minimizing player *)
        value := +∞
        for each child of node do
            value := min(value, minimax(child, depth − 1, TRUE))
        return value

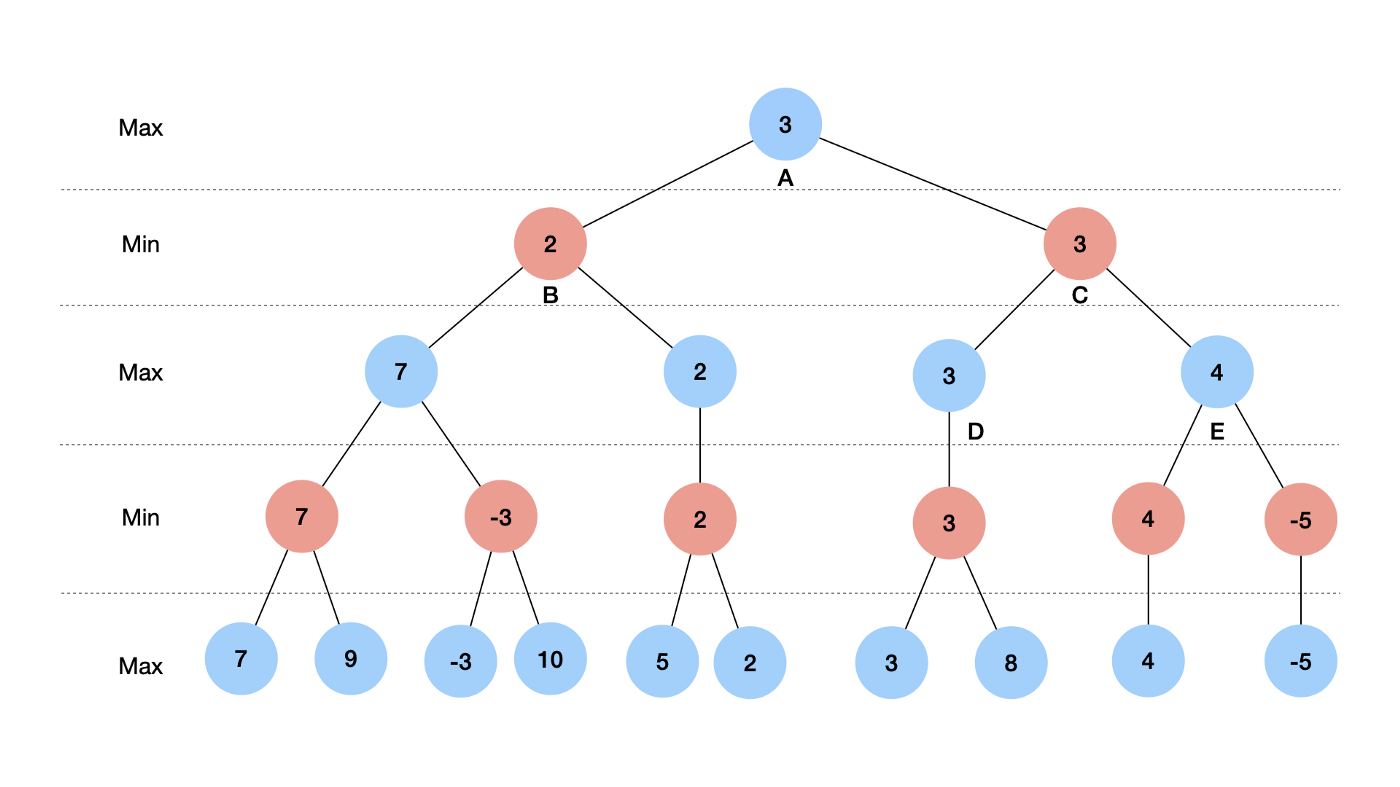
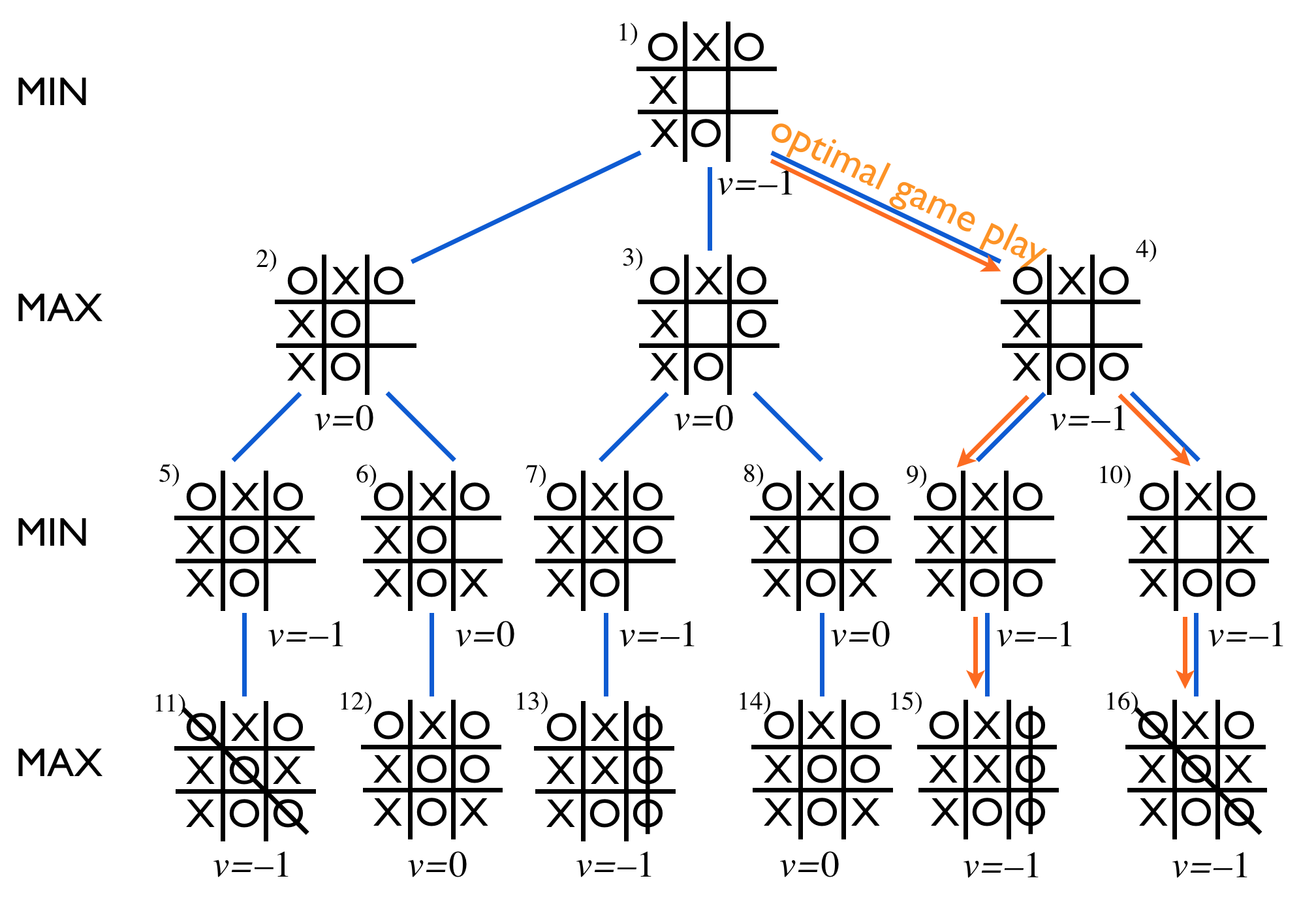
图解算法：实际上就是决策树的遍历过程

实例代码 - Go 语言

minimax 算法游戏 AI

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
package main
​
import "fmt"
​
// 走法结构体
type Move struct {
    row, col int
}
​
// 评价函数
func evaluate(board [3][3]byte) int {
    // Rows
    for row := 0; row < 3; row++ {
        if board[row][0] == board[row][1] && board[row][1] == board[row][2] {
            if board[row][0] == 'x' {
                return 1
            }
            if board[row][0] == 'o' {
                return -1
            }
        }
    }
    // Colums
    for col := 0; col < 3; col++ {
        if board[0][col] == board[1][col] && board[1][col] == board[2][col] {
            if board[0][col] == 'x' {
                return 1
            }
            if board[0][col] == 'o' {
                return -1
            }
        }
    }
    // Diagonals
    if board[0][0] == board[1][1] && board[1][1] == board[2][2] {
        if board[0][0] == 'x' {
            return 1
        }
        if board[0][0] == 'o' {
            return -1
        }
    }
    if board[0][2] == board[1][1] && board[1][1] == board[2][0] {
        if board[0][2] == 'x' {
            return 1
        }
        if board[0][2] == 'o' {
            return -1
        }
    }
    return 0
}
​
// minimax函数
func minimax(board [3][3]byte, isMax bool) int {
    score := evaluate(board)
    if score != 0 {
        return score
    }
    if isFull(board) {
        return 0
    }
​    // 回合判断
    if isMax {
        maxVal := -10
        for row := 0; row < 3; row++ {
            for col := 0; col < 3; col++ {
                if board[row][col] == '-' {
                    board[row][col] = 'x'
                    maxVal = max(maxVal, minimax(board, !isMax))
                    board[row][col] = '-'
                }
            }
        }
        return maxVal
    } else {
        minVal := 10
        for row := 0; row < 3; row++ {
            for col := 0; col < 3; col++ {
                if board[row][col] == '-' {
                    board[row][col] = 'o'
                    minVal = min(minVal, minimax(board, !isMax))
                    board[row][col] = '-'
                }
            }
        }
        return minVal
    }
}
​
// 最佳走法函数
func bestMove(board [3][3]byte) Move {
    var move Move
    move.row, move.col = -1, -1
    minVal := 10
    for row := 0; row < 3; row++ {
        for col := 0; col < 3; col++ {
            if board[row][col] == '-' {
                board[row][col] = 'o'
                moveVal := minimax(board, true)
                board[row][col] = '-'
                if moveVal < minVal {
                    move.row = row
                    move.col = col
                    minVal = moveVal
                }
            }
        }
    }
    fmt.Println()
    return move
}
​
// 判断是否棋盘已满
func isFull(board [3][3]byte) bool {
    for row := 0; row < 3; row++ {
        for col := 0; col < 3; col++ {
            if board[row][col] == '-' {
                return false
            }
        }
    }
    return true
}
​
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}
​
func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

主程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
package main
​
import "fmt"
​
// 游戏状态结构体
type GameState struct {
    board [3][3]byte
}
​
// 判断是否为空棋格
func isEmpty(board [3][3]byte, row, col int) bool {
    if board[row][col] == '-' {
        return true
    }
    return false
}
​
// 判断是否获胜
func isWin(board [3][3]byte) bool {
    // Rows
    for row := 0; row < 3; row++ {
        if board[row][0] == board[row][1] && board[row][1] == board[row][2] && board[row][0] != '-' {
            return true
        }
    }
    // Colums
    for col := 0; col < 3; col++ {
        if board[0][col] == board[1][col] && board[1][col] == board[2][col] && board[0][col] != '-' {
            return true
        }
    }
    // Diagonals
    if board[0][0] == board[1][1] && board[1][1] == board[2][2] && board[0][0] != '-' {
        return true
    }
    if board[0][2] == board[1][1] && board[1][1] == board[2][0] && board[0][2] != '-' {
        return true
    }
    return false
}
​
// 判断是否游戏结束
func isEnd(board [3][3]byte) bool {
    if isWin(board) {
        return true
    }
    for row := 0; row < 3; row++ {
        for col := 0; col < 3; col++ {
            if isEmpty(board, row, col) {
                return false
            }
        }
    }
    return true
}
​
// 显示棋盘状态
func showBoard(board [3][3]byte) {
    for row := 0; row < 3; row++ {
        for col := 0; col < 3; col++ {
            fmt.Printf("%c ", board[row][col])
        }
        fmt.Println()
    }
}
​
func main() {
    var gs GameState
    gs.board = [3][3]byte{
        {'-', '-', '-'},
        {'-', '-', '-'},
        {'-', '-', '-'},
    }
    showBoard(gs.board)
    var row, col int
    for !isEnd(gs.board) {
        fmt.Scanf("%d %d", &row, &col)
        if isEmpty(gs.board, row, col) {
            gs.board[row][col] = 'x'
            showBoard(gs.board)
            fmt.Println()
            if isEnd(gs.board) {
                fmt.Println("Game Over")
                break
            }
            oMove := bestMove(gs.board)
            gs.board[oMove.row][oMove.col] = 'o'
            showBoard(gs.board)
            fmt.Println("-------------------------------------------------------------------------------------------")
        }
    }
}

控制台

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
- - - 
- - -
- - -
1 1
- - - 
- x -
- - -
​
o - -
- x -
- - -
-----------------------------------------------------------------------------------------------------------------------
2 0
o - - 
- x -
x - -

o - o
- x -
x - -
-----------------------------------------------------------------------------------------------------------------------
2 2
o - o 
- x -
x - x
​
o o o
- x -
x - x
-----------------------------------------------------------------------------------------------------------------------